import math
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
import GPy
import jax
import gpytorch
import botorch
import tinygp
import jax.numpy as jnp
import optax
from IPython.display import clear_output

from sklearn.preprocessing import StandardScaler

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

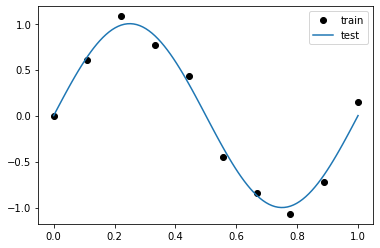
Data

np.random.seed(0) # We don't want surprices in a presentation :)
N = 10
train_x = torch.linspace(0, 1, N)
train_y = torch.sin(train_x * (2 * math.pi)) + torch.normal(0, 0.1, size=(N,))
 
test_x = torch.linspace(0, 1, N*10)
test_y = torch.sin(test_x * (2 * math.pi))

plt.plot(train_x, train_y, 'ko', label='train');
plt.plot(test_x, test_y, label='test');
plt.legend();

Defining kernel

\[\begin{equation} \sigma_f^2 = \text{variance}\\ \ell = \text{lengthscale}\\ k_{RBF}(x_1, x_2) = \sigma_f^2 \exp \left[-\frac{\lVert x_1 - x_2 \rVert^2}{2\ell^2}\right] \end{equation}\]

GPy

gpy_kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.)
gpy_kernel

rbf.	value	constraints	priors
variance	1.0	+ve
lengthscale	1.0	+ve

GPyTorch

gpytorch_kernel = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
gpytorch_kernel.outputscale = 1. # variance
gpytorch_kernel.base_kernel.lengthscale = 1. # lengthscale

gpytorch_kernel

ScaleKernel(
  (base_kernel): RBFKernel(
    (raw_lengthscale_constraint): Positive()
  )
  (raw_outputscale_constraint): Positive()
)

TinyGP

def RBFKernel(variance, lengthscale):
    return jnp.exp(variance) * tinygp.kernels.ExpSquared(scale=jnp.exp(lengthscale))
    
tinygp_kernel = RBFKernel(variance=1., lengthscale=1.)
tinygp_kernel

<tinygp.kernels.Product at 0x7f544039d710>

Define model

\[ \sigma_n^2 = \text{noise variance} \]

GPy

gpy_model = GPy.models.GPRegression(train_x.numpy()[:,None], train_y.numpy()[:,None], gpy_kernel)
gpy_model.Gaussian_noise.variance = 0.1
gpy_model

Model: GP regression
Objective: 16.757933772959404
Number of Parameters: 3
Number of Optimization Parameters: 3
Updates: True

GP_regression.	value	constraints	priors
rbf.variance	1.0	+ve
rbf.lengthscale	1.0	+ve
Gaussian_noise.variance	0.1	+ve

GPyTorch

class ExactGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood, kernel):
        super().__init__(train_x, train_y, likelihood)
        
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = kernel

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

gpytorch_likelihood = gpytorch.likelihoods.GaussianLikelihood()
gpytorch_model = ExactGPModel(train_x, train_y, gpytorch_likelihood, gpytorch_kernel)

gpytorch_model.likelihood.noise = 0.1
gpytorch_model

ExactGPModel(
  (likelihood): GaussianLikelihood(
    (noise_covar): HomoskedasticNoise(
      (raw_noise_constraint): GreaterThan(1.000E-04)
    )
  )
  (mean_module): ConstantMean()
  (covar_module): ScaleKernel(
    (base_kernel): RBFKernel(
      (raw_lengthscale_constraint): Positive()
    )
    (raw_outputscale_constraint): Positive()
  )
)

TinyGP

def build_gp(theta, X):
    mean = theta[0] 
    variance, lengthscale, noise_variance = jnp.exp(theta[1:])
    
    kernel = variance * tinygp.kernels.ExpSquared(lengthscale)
    
    return tinygp.GaussianProcess(kernel, X, diag=noise_variance, mean=mean)

tinygp_model = build_gp(theta=np.array([0., 1., 1., 0.1]), X=train_x.numpy())

tinygp_model
# __repr__

<tinygp.gp.GaussianProcess at 0x7f5440401850>

Train the model

GPy

gpy_model.optimize(max_iters=50)
gpy_model

Model: GP regression
Objective: 3.944394423452163
Number of Parameters: 3
Number of Optimization Parameters: 3
Updates: True

GP_regression.	value	constraints	priors
rbf.variance	0.9376905183253631	+ve
rbf.lengthscale	0.2559000163858406	+ve
Gaussian_noise.variance	0.012506184441481319	+ve

GPyTorch

mll = gpytorch.mlls.ExactMarginalLogLikelihood(gpytorch_likelihood, gpytorch_model)
botorch.fit_gpytorch_model(mll)

display(gpytorch_model.mean_module.constant, # Mean
        gpytorch_model.covar_module.outputscale, # Variance
        gpytorch_model.covar_module.base_kernel.lengthscale, # Lengthscale 
        gpytorch_model.likelihood.noise) # Noise variance

 /opt/conda/lib/python3.7/site-packages/botorch/fit.py:143: UserWarning:CUDA initialization: CUDA unknown error - this may be due to an incorrectly set up environment, e.g. changing env variable CUDA_VISIBLE_DEVICES after program start. Setting the available devices to be zero. (Triggered internally at  /opt/conda/conda-bld/pytorch_1634272168290/work/c10/cuda/CUDAFunctions.cpp:112.)

Parameter containing:
tensor([0.0923], requires_grad=True)

tensor(0.9394, grad_fn=<SoftplusBackward0>)

tensor([[0.2560]], grad_fn=<SoftplusBackward0>)

tensor([0.0124], grad_fn=<AddBackward0>)

TinyGP

from scipy.optimize import minimize

def neg_log_likelihood(theta, X, y):
    gp = build_gp(theta, X)
    return -gp.condition(y)


obj = jax.jit(jax.value_and_grad(neg_log_likelihood))
result = minimize(obj, [0., 1., 1., 0.1], jac=True, args=(train_x.numpy(), train_y.numpy()))
result.x[0], np.exp(result.x[1:])

(0.09213499552879165, array([0.9395271 , 0.25604163, 0.01243025]))

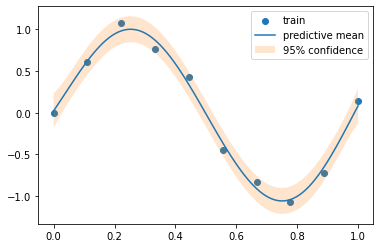
Inference

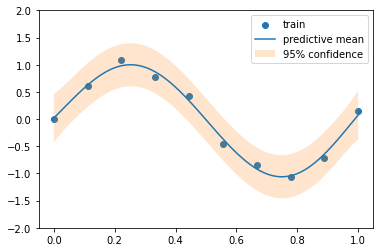
def plot_gp(pred_y, var_y):
    std_y = var_y ** 0.5
    plt.figure()
    plt.scatter(train_x, train_y, label='train')
    plt.plot(test_x, pred_y, label='predictive mean')
    plt.fill_between(test_x.ravel(), 
                     pred_y.ravel() - 2*std_y.ravel(), 
                     pred_y.ravel() + 2*std_y.ravel(), alpha=0.2, label='95% confidence')
    plt.legend()

GPy

pred_y, var_y = gpy_model.predict(test_x.numpy()[:, None])
plot_gp(pred_y, var_y)

GPyTorch

gpytorch_model.eval()

with torch.no_grad(), gpytorch.settings.fast_pred_var():
    pred_dist = gpytorch_likelihood(gpytorch_model(test_x))
    pred_y, var_y = pred_dist.mean, pred_dist.variance
    plot_gp(pred_y, var_y)

TinyGP

tinygp_model = build_gp(result.x, train_x.numpy())
pred_y, var_y = tinygp_model.predict(train_y.numpy(), test_x.numpy(), return_var=True)

plot_gp(pred_y, var_y)

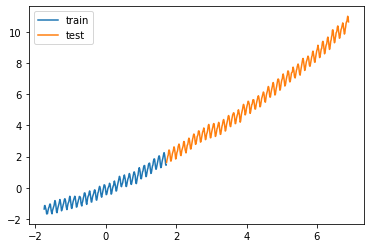
Tiny GP on CO2 dataset

data = pd.read_csv("data/co2.csv")

# Train test split
X = data["0"].iloc[:290].values.reshape(-1, 1)
X_test = data["0"].iloc[290:].values.reshape(-1, 1)
y = data["1"].iloc[:290].values
y_test = data["1"].iloc[290:].values

# Scaling the dataset
Xscaler = StandardScaler()
X = Xscaler.fit_transform(X)
X_test = Xscaler.transform(X_test)

yscaler = StandardScaler()
y = yscaler.fit_transform(y.reshape(-1, 1)).ravel()
y_test = yscaler.transform(y_test.reshape(-1, 1)).ravel()

plt.plot(X, y, label='train');
plt.plot(X_test, y_test, label='test');
plt.legend();

class SpectralMixture(tinygp.kernels.Kernel):
    def __init__(self, weight, scale, freq):
        self.weight = jnp.atleast_1d(weight)
        self.scale = jnp.atleast_1d(scale)
        self.freq = jnp.atleast_1d(freq)

    def evaluate(self, X1, X2):
        tau = jnp.atleast_1d(jnp.abs(X1 - X2))[..., None]
        return jnp.sum(
            self.weight
            * jnp.prod(
                jnp.exp(-2 * jnp.pi ** 2 * tau ** 2 / self.scale ** 2)
                * jnp.cos(2 * jnp.pi * self.freq * tau),
                axis=-1,
            )
        )
    
def build_spectral_gp(theta):
    kernel = SpectralMixture(
        jnp.exp(theta["log_weight"]),
        jnp.exp(theta["log_scale"]),
        jnp.exp(theta["log_freq"]),
    )
    return tinygp.GaussianProcess(
        kernel, X, diag=jnp.exp(theta["log_diag"]), mean=theta["mean"]
    )

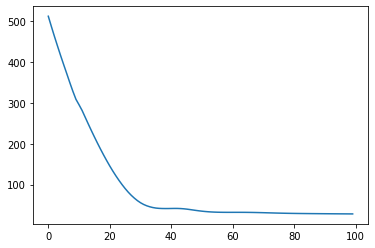
K = 4 # Number of mixtures
div_factor = 0.4
np.random.seed(1)
params = {
    "log_weight": np.abs(np.random.rand(K))/div_factor,
    "log_scale": np.abs(np.random.rand(K))/div_factor,
    "log_freq": np.abs(np.random.rand(K))/div_factor,
    "log_diag": np.abs(np.random.rand(1))/div_factor,
    "mean": 0.,
}

@jax.jit
@jax.value_and_grad
def loss(theta):
    return -build_spectral_gp(theta).condition(y)
# opt = optax.sgd(learning_rate=0.001)
opt = optax.adam(learning_rate=0.1)
opt_state = opt.init(params)
losses = []
for i in range(100):
    loss_val, grads = loss(params)
    updates, opt_state = opt.update(grads, opt_state)
    params = optax.apply_updates(params, updates)
    losses.append(loss_val)
    clear_output(wait=True)
    print(f"iter {i}, loss {loss_val}")

opt_gp = build_spectral_gp(params)

params

iter 99, loss 27.987701416015625

{'log_diag': DeviceArray([-2.7388687], dtype=float32),
 'log_freq': DeviceArray([-3.6072493, -3.1795945, -3.4490397, -2.373117 ], dtype=float32),
 'log_scale': DeviceArray([3.9890492, 3.8530042, 4.0878096, 4.4860597], dtype=float32),
 'log_weight': DeviceArray([-1.3715047, -0.6132469, -2.413771 , -1.6582283], dtype=float32),
 'mean': DeviceArray(0.38844627, dtype=float32)}

plt.plot(losses);

mu, var = opt_gp.predict(y, X_test, return_var=True)

plt.plot(X, y, c='k')
plt.fill_between(
    X_test.ravel(), mu + np.sqrt(var), mu - np.sqrt(var), color="C0", alpha=0.5
)
plt.plot(X_test, mu, color="C0", lw=2)

# plt.xlim(t.min(), 2025)
plt.xlabel("year")
_ = plt.ylabel("CO$_2$ in ppm")

Idea

\(K_\mathbf{y} = \text{cov_function}(X_{train}, X_{train}, \sigma_f, \ell, \sigma_n)\)

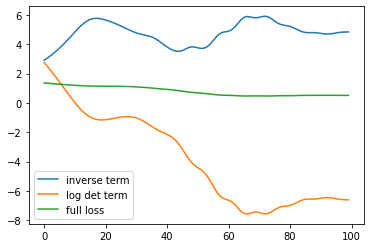
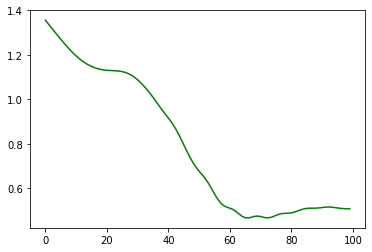
GP Loss: \(\log p(\mathbf{y} \mid \mathbf{X}, \theta)=-\frac{1}{2} \mathbf{y}^{T} K_{y}^{-1} \mathbf{y}-\frac{1}{2} \log \left|K_{y}\right|-\frac{n}{2} \log 2 \pi\)

Minimize inverse term fully
Now, Minimize both togather

Appendix

gp_model = ExactGPModel(train_x, train_y, gpytorch.likelihoods.GaussianLikelihood(), 
                        gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel()))
zmll = gpytorch.ExactMarginalLogLikelihood(gp_model.likelihood, gp_model)

def loss1(model, x, y):
    l = torch.cholesky(model.likelihood(model(x)).covariance_matrix)
    alp = torch.cholesky_solve(y.reshape(-1,1), l)
    return (y.reshape(-1,1).T@alp).ravel()

def loss_det(model, x, y):
    l = torch.cholesky(model.likelihood(model(x)).covariance_matrix)
    return torch.log(l.diagonal()).sum()

def loss_full(model, x, y):
    dist = model(x)
    return -zmll(dist, y)

zopt = torch.optim.Adam(gp_model.parameters(), lr=0.1)
torch.manual_seed(0)
for p in gp_model.parameters():
    torch.nn.init.normal_(p)

zlosses1 = []
zlosses2 = []
zlosses = []
for i in range(100):
    clear_output(True)
    print(i)
    zopt.zero_grad()
    zloss = 0
    zloss = zloss + loss1(gp_model, train_x, train_y)
    zloss = zloss + loss_det(gp_model, train_x, train_y)
    zloss.backward()
    zopt.step()
    zlosses1.append(loss1(gp_model, train_x, train_y).item())
    zlosses2.append(loss_det(gp_model, train_x, train_y).item())
    zlosses.append(loss_full(gp_model, train_x, train_y).item())
# for i in range(100):
#     clear_output(True)
#     print(i)
#     zopt.zero_grad()
#     zloss = 0
#     zloss = zloss + loss_det(gp_model, train_x, train_y)
#     zloss = zloss + loss1(gp_model, train_x, train_y)
#     zloss.backward()
#     zopt.step()
#     zlosses.append(loss2(gp_model, train_x, train_y).item())
    
plt.plot(zlosses1, label='inverse term');
plt.plot(zlosses2, label='log det term');
plt.plot(zlosses, label='full loss');
plt.legend();
plt.figure()
plt.plot(zlosses, c='g');

gp_model.eval()
with torch.no_grad(), gpytorch.settings.fast_pred_var():
    pdist = gp_model.likelihood(gp_model(test_x))
    plot_gp(pdist.mean, pdist.variance);
    plt.ylim(-2,2)